Формула закона ома для цепи переменного тока — представление, применение и особенности расчета

В мире электричества существует особенное явление, которое позволяет нам передавать энергию и информацию по проводам, держать в наших руках магические устройства и ощущать себя безмятежными потребителями технологического прогресса. Секрет этого феномена заключается в формуле, которая является основой для понимания работы цепи переменного тока.

Столь широко используемая и глубоко вкорененная в мир науки формула, в основе своей, описывает ни что иное, как закон, который устанавливает пропорциональность между разностью потенциалов на концах цепи и током, протекающем через нее. Это позволяет нам понять, как электрический ток перемещается по проводам, внутри схем и устройств, и какая сила приводит его в движение.

Суть этого закона заключается не только в установлении связи между физическими значениями, но и в объяснении причинно-следственных связей, возникающих при передаче электрической энергии. Он является фундаментальным принципом работы электрических цепей и позволяет нам разрабатывать и улучшать системы энергоснабжения, создавать эффективное освещение и передавать информацию на все большие расстояния.

Глубже погрузившись в этот захватывающий мир электрических цепей и переменного тока, мы обнаружим, что формула этого закона не только позволяет нам рассчитывать ток и напряжение, но и устанавливает связь сопротивления цепи, частоты тока и ёмкости конденсаторов. Таким образом, формула становится неотъемлемой частью нашего понимания процессов, происходящих в электрических схемах и устройствах.

Физический принцип, описывающий электрическое поведение в переменной цепи

Теоретические основы и общие принципы

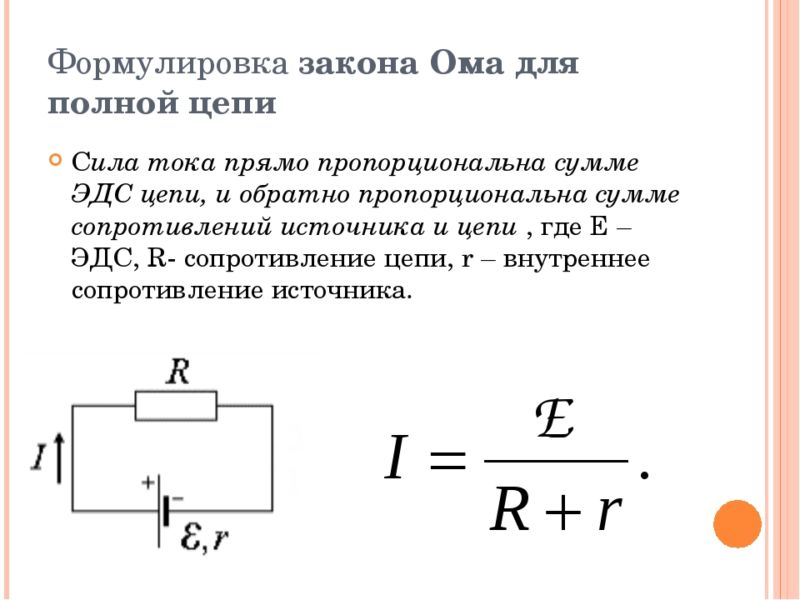
В данном разделе рассматриваются фундаментальные концепции и принципы, лежащие в основе формулы закона Ома для электрической цепи переменного тока. Здесь мы сделаем обзор ключевых аспектов, которые помогут нам лучше понять электрическую систему и ее взаимодействие с переменным током.

Закон Ома является одним из основных законов в электротехнике и описывает зависимость между током, напряжением и сопротивлением в электрической цепи. Он формулирует связь между переменным током, протекающим через цепь, и напряжением, присутствующим в данной цепи. Для полного понимания закона Ома необходимо усвоить теоретические основы, к которым относятся понятия электрического тока, напряжения и сопротивления.

Ключевые концепции, которые мы рассмотрим, включают определения тока, напряжения и сопротивления, а также важные принципы, касающиеся взаимодействия переменного тока с элементами электрической цепи. Мы также рассмотрим роль реактивных элементов в переменных электрических цепях и их влияние на общую схему.

Понимание этих теоретических основ и общих принципов является важным шагом для более глубокого изучения формулы закона Ома для цепи переменного тока. Грамотное усвоение основных понятий и принципов позволит нам более четко воспринимать материал, связанный с этой темой, и изучать более сложные концепции, углубляясь в электротехническую науку.

Переменный ток и его свойства

Раздел рассматривает основные характеристики переменного тока, форму своего протекания и его взаимодействие с электрическими цепями. Понимание этих свойств позволит нам лучше понять основы закона Ома, который определяет зависимость между током, напряжением и сопротивлением в цепи переменного тока.

При работе с переменным током важно учитывать его основные характеристики. Например, переменный ток по своей природе меняет свое направление и амплитуду со временем. Это значит, что ток в цепи может меняться как по величине, так и по направлению своего течения. Этот факт отличает переменный ток от постоянного, который имеет постоянную величину и направление.

• Одной из ключевых характеристик переменного тока является его частота, которая измеряется в герцах (Гц). Частота определяет количество изменений направления тока за единицу времени.
• Еще одной важной характеристикой является амплитуда переменного тока, которая определяет его максимальное значение в каждом изменении направления.
• Переменный ток также обладает фазой, которая указывает на относительное смещение между током и напряжением в цепи.
• Важно отметить, что переменный ток может быть непостоянным и иметь различную форму своего изменения, такую как синусоида, пила, треугольник и другие.

Понимание этих характеристик переменного тока поможет нам разобраться в законе Ома для цепи переменного тока, который определяет зависимость между током, напряжением и сопротивлением при изменяющемся токе в электрической цепи.

б) Основные концепции в электрической цепи

В электротехнике существуют основные понятия, которые необходимо понимать при изучении закона ома для цепи переменного тока. Эти понятия помогают описать и объяснить свойства и поведение электрических цепей.

Одним из основных понятий является сопротивление, которое характеризует сложность движения электрического тока через материал или элемент в цепи. Сопротивление обусловлено сопротивлением материала, его геометрией и физическими свойствами.

Другим важным понятием является электрическое напряжение, которое представляет собой разность потенциалов между двумя точками в цепи. Оно создается источником электричества и приводит к движению электрического тока в цепи.

Третье понятие — электрический ток, представляет собой движение зарядов по проводнику в результате действия электрического поля. Ток имеет направление и величину и может быть постоянным (постоянного направления) или переменным (сменяющего направление).

Кроме того, в цепи встречаются понятия активного сопротивления (характеризующего действительную часть импеданса), реактивного сопротивления (характеризующего мнимую часть импеданса), а также импеданса (комплексного сопротивления, учитывающего влияние взаимодействия активного и реактивного сопротивлений).

Понятие	Описание
Сопротивление	Характеризует сложность движения электрического тока в цепи
Электрическое напряжение	Разность потенциалов между двуми точками в цепи
Электрический ток	Движение зарядов по проводнику в результате действия электрического поля
Активное сопротивление	Действительная часть импеданса, характеризующая активные потери энергии в цепи
Реактивное сопротивление	Мнимая часть импеданса, характеризующая энергетические потери, связанные с электрическим и магнитным полями
Импеданс	Комплексное сопротивление, учитывающее влияние активного и реактивного сопротивлений

Применение формулы в реальных расчетах

В данном разделе рассмотрим практическое использование формулы, которая описывает зависимость между различными величинами в схемах переменного тока. Обратим внимание на то, как эта формула может быть применена для решения разнообразных задач и проведения расчетов.

С помощью данной формулы и сопутствующих уравнений, можно определить важные параметры схемы, такие как сила тока, напряжение, сопротивление и мощность. Такие расчеты могут быть полезны при проектировании электрических цепей, а также в работе с устройствами, использующими переменный ток.

Таблица ниже демонстрирует различные сценарии использования формулы в практических расчетах:

Сценарий	Применение формулы
Расчет сопротивления	Используя формулу, можно определить сопротивление элемента схемы путем измерения тока и напряжения на нем.
Расчет мощности	Формула позволяет вычислить мощность, выделяемую в цепи, используя известные значения тока и напряжения.
Расчет тока	С использованием формулы можно определить силу тока, проходящую через элемент схемы, если известно его сопротивление и напряжение.

Как видно из таблицы, формула оказывается полезной для решения различных задач и облегчает практические расчеты в схемах переменного тока. Зная значения тока, напряжения и сопротивления, мы можем определить необходимые параметры и эффективно работать с электрическими цепями.

Анализирование сопротивления электрического тока

В данном разделе представлено исследование процесса расчета сопротивления электрического тока в цепи переменного напряжения. Сопротивление представляет собой физическую характеристику, которая препятствует свободному движению зарядов. Величина сопротивления зависит от характеристик материала, из которого состоит проводник, его геометрии и температуры.

Вначале установим связь между силой, напряжением и током. Величина сопротивления определяется через закон Ома, который утверждает, что сила тока пропорциональна разности потенциалов на концах проводника. В случае переменного тока, сопротивление может быть переменным и зависит от частоты, амплитуды и фазы тока.

Определение сопротивления тока требует выполнения нескольких шагов. В первую очередь, необходимо измерить напряжение на цепи и затем текущую силу. Далее, используя формулу сопротивления, можно вычислить его численное значение. В общем случае, сопротивление имеет единицы ома (Ом) и обозначается символом R.

• Выберите подходящую схему измерений, учитывая характеристики цепи и доступное оборудование.
• Примените вольтметр для измерения напряжения на цепи.
• Используйте амперметр для измерения текущей силы в цепи.
• Подставьте измеренные значения в формулу сопротивления и произведите необходимые вычисления.

Таким образом, расчет сопротивления электрического тока является важной задачей в области электротехники. Правильное определение сопротивления позволяет анализировать и прогнозировать поведение электрических цепей, а также проектировать электронные устройства с требуемыми характеристиками.

Примеры применения электрических схем с учетом закона возникновения и изменения электрического тока

Рассмотрим некоторые интересные случаи применения формулы статистического закона проводимости электростатически мобильных зарядов, который позволяет оценить величину тока в электрической цепи.

Одним из таких примеров является использование закона поведения зарядов в конденсаторах. Конденсаторы, лежащие в разных частях цепи, могут быть соединены параллельно или последовательно. Закон омического поведения позволяет определить ток, протекающий через конденсаторы в разных конфигурациях и понять, как изменится ток в каждом конденсаторе при изменении параметров цепи.

Вторым примером является использование закона проводимости в индуктивных элементах цепи. Индуктивность обусловлена возникновением электромагнитного поля при протекании тока через катушку или катушку с сердечником. Используя формулу закона омического приведения катушки, можно определить величину тока и связанные с ним характеристики магнитного поля, такие как магнитная индукция и магнитная энергия.

Третий пример применения закона проводимости связан с использованием полупроводниковых элементов в электрических схемах. Полупроводники, такие как диоды и транзисторы, позволяют контролировать поток электронов и дырок в цепи, влияя на величину тока и напряжения. Формула закона омической проводимости полупроводниковых элементов позволяет оценить эффективность использования таких элементов в электрических цепях и определить их влияние на общую работу устройства.

Приведенные примеры подчеркивают важность понимания и применения закона омического проводимости в различных электрических схемах. Знание этого закона позволяет инженерам и научным исследователям разрабатывать эффективные и безопасные электрические устройства, а также оптимизировать их работу в соответствии с требованиями и задачами.

Особенности применения формулы ома при переменном токе

При использовании формулы ома в контексте переменного тока следует учитывать ряд особенностей, которые отличаются от применения этой формулы в контексте постоянного тока.

Временные изменения напряжения и сопротивления: В отличие от статичного постоянного тока, при работе со переменным током напряжение и сопротивление могут меняться со временем. Это означает, что значения переменного тока и сопротивления могут значительно колебаться, влияя на эффективность и результаты расчетов.

Учет реактивного сопротивления: Переменный ток вызывает эффект индукции и взаимодействия поля постоянного и переменного тока. Это приводит к появлению реактивного сопротивления, которое необходимо учитывать при применении формулы ома. Реактивное сопротивление вводит понятие активной и реактивной мощности, что требует более сложных вычислений и анализа.

Работа с комплексными числами: Для учета фазовых сдвигов и взаимосвязи между током и напряжением в переменном токе используются комплексные числа. Формула ома для переменного тока применяется в комплексной форме, где сопротивление представляется как комплексное число, а величина тока и напряжения имеют как активную, так и реактивную составляющую.

Настраиваемость системы: Применение формулы ома для переменного тока позволяет настраивать систему с учетом электрических параметров, таких как частота и амплитуда переменного тока. Это может быть полезно при проектировании и оптимизации электрических цепей при работе с переменным током.

Видео: