Закон Ома для пассивного участка цепи: основы и применение

Закон ома для пассивного участка цепи

В мире электроники и электрической инженерии особое внимание уделяется пассивным элементам, играющим важную роль в управлении током и напряжением в электрических цепях. Все эти элементы подчиняются основным правилам и закономерностям, которые диктует закон Ома для пассивного участка цепи.

Закон Ома даёт возможность оценить и предсказать поведение электрического тока и напряжения в цепи на основе таких параметров, как сопротивление, проводимость и электрическая мощность. Этот закон находит широкое применение в различных областях электротехники, включая дизайн и анализ электрических схем, разработку электронных устройств и систем, а также в исследованиях с целью оптимизации энергопотребления.

С наступлением эпохи цифровой индустрии и развитием технологий, роль пассивных элементов только возросла. Миллионы микро- и наносхем, а также простых электрических устройств содержат различные пассивные элементы, такие как резисторы, конденсаторы и катушки индуктивности. Они выполняют различные функции, от стабилизации напряжения до фильтрации шума и сглаживания сигналов.

В этой статье мы рассмотрим основные принципы, лежащие в основе работы пассивного элемента в электрической цепи, и изучим, как взаимодействие этого элемента с другими компонентами влияет на общую производительность цепи. Мы также рассмотрим некоторые примеры практического применения закона Ома и его важность для достижения эффективности и стабильности в электрической инженерии.

Содержание

Сущность работы пассивного участка цепи согласно принципу Ома

Рассмотрим важный аспект работы системы электрической цепи, который подчиняется основному принципу, называемому законом Ома. В определенных условиях пассивный участок цепи способен изменять ток, проходящий через него, в соответствии с напряжением, причем это изменение происходит прямо пропорционально сопротивлению данного участка.

Влияние сопротивления на пассивный участок цепи

Сопротивление – это физическая величина, которая ограничивает поток электрического тока в цепи. В пассивном участке цепи, значение сопротивления влияет на электрические параметры данного участка. Высокое сопротивление ограничивает ток, что в свою очередь приводит к снижению энергии, расходуемой на данном участке. Низкое сопротивление, напротив, способствует пропусканию большего количества тока, что увеличивает энергию и мощность данного участка.

Связь между напряжением и током на пассивном участке цепи

Согласно закону Ома, напряжение, поданное на пассивный участок цепи, пропорционально току, протекающему через него. То есть, увеличение напряжения приведет к увеличению тока на данном участке, а уменьшение напряжения — к уменьшению тока. Данная связь позволяет электрическим системам управлять и регулировать токи, которые протекают через пассивный участок цепи, с помощью изменения напряжения на этом участке.

Сопротивление	Напряжение	Ток
Высокое	Снижается	Ограничивается
Низкое	Увеличивается	Увеличивается

Роль формулы сопротивления в анализе поведения пассивных компонентов электрической цепи

Электрические цепи состоят из различных компонентов, которые выполняют разные функции. Пассивные элементы, такие как резисторы, конденсаторы и индуктивности, играют важную роль в передаче и преобразовании электрической энергии. Для анализа и понимания поведения этих компонентов используется формула сопротивления, которая позволяет определить их электрическое поведение и предсказать результаты приложения электрического тока или напряжения.

Принцип формулы сопротивления

Формула сопротивления включает в себя несколько важных понятий, таких как сопротивление, напряжение и ток. Сопротивление — это электрический параметр, обозначающий степень сопротивления материала току проходить через него. Напряжение — это разность потенциалов между двумя точками электрической цепи, а ток — это электрический заряд, протекающий через цепь за определенное время. Формула сопротивления позволяет выразить сопротивление через напряжение и ток, применяя математическое отношение между этими тремя параметрами. Таким образом, формула сопротивления является важным инструментом для анализа и понимания поведения пассивных элементов цепи.

Применение формулы сопротивления

Применение формулы сопротивления позволяет установить связь между физическими характеристиками пассивных элементов цепи и электрическими параметрами, такими как напряжение и ток. Путем применения формулы сопротивления можно определить электрическое поведение конкретного пассивного элемента: как он будет реагировать на ток или напряжение и какие эффекты это может вызвать в цепи в целом. Например, формула сопротивления позволяет определить, какое количество энергии будет рассеиваться в виде тепла при прохождении тока через резистор или как изменится напряжение на конденсаторе в зависимости от тока, протекающего через него. Таким образом, применение формулы сопротивления является необходимым инструментом для эффективного проектирования и анализа электрических цепей с использованием пассивных компонентов.

Связь между сопротивлением, напряжением и силой тока: ключевые аспекты

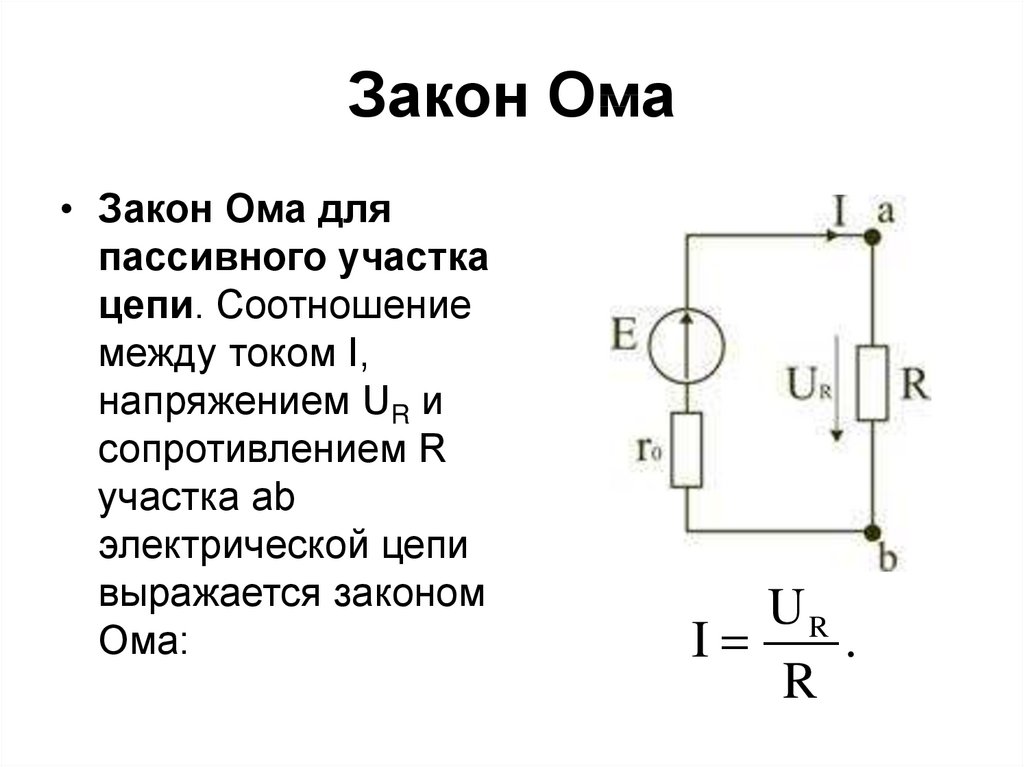
В этом разделе мы рассмотрим фундаментальную связь между сопротивлением, напряжением и силой тока в контексте пассивного участка электрической цепи. От простых идей о сопротивлении и напряжении до более глубокого понимания тока, мы проанализируем и объясним, как эти параметры взаимосвязаны и как они влияют на работу участка цепи.

Сопротивление: препятствие движению электрического тока

Сопротивление в электрической цепи можно представить как препятствие, которое осложняет свободное движение электрического тока. Чем больше сопротивление в цепи, тем больше усилий требуется для преодоления этого препятствия и тем меньше тока будет протекать. Сопротивление измеряется в омах и зависит от материала, геометрии и других свойств компонентов цепи.

Напряжение: драйвер движения электрического тока

Напряжение в электрической цепи может быть описано как сила или драйвер, побуждающая электрический ток к движению. Высокое напряжение создает сильный потенциал для движения тока, в то время как низкое напряжение ограничивает его поток. Напряжение измеряется в вольтах и может быть создано источником питания или другими электрическими устройствами.

Сопротивление и напряжение прямо взаимосвязаны: чем больше сопротивление, тем больше напряжение требуется для поддержания определенной силы тока, и наоборот.
Сила тока: результат взаимодействия сопротивления и напряжения

Сила тока, или электрический ток, представляет собой результат взаимодействия между сопротивлением и напряжением в цепи. Представленная в амперах, она определяет количество заряда, проходящего через участок цепи за единицу времени. Главное о чем нужно помнить — чем больше напряжение или меньше сопротивление, тем сильнее будет ток. Таким образом, сопротивление, напряжение и сила тока образуют сложную зависимость, которая определяет поведение и производительность электрической цепи.

Применимость закона Ома к резисторам, индуктивностям и конденсаторам.

Резисторы

Резисторы являются п passivelyассивными элементами цепи, которые создают сопротивление для потока электрического тока. В соответствии с законом Ома, сила тока, протекающего через резистор, пропорциональна напряжению, приложенному к нему. Сопротивление резистора определяет эту пропорциональность и является величиной, обратной удельной проводимости элемента.

Индуктивности

Индуктивности, или катушки, обладают свойством индуктивности, то есть способностью генерировать электрическое напряжение при изменении тока, протекающего через них. Закон Ома применим к индуктивностям, но с учетом включения дополнительного влияния индуктивности на поведение цепи. В данном случае, напряжение на индуктивности вычисляется как произведение индуктивности на изменение тока во времени, а сила тока через индуктивность определяется взаимодействием сопротивления этого элемента и приложенного напряжения.

Конденсаторы

Конденсаторы представляют собой емкостные элементы, способные накапливать заряд при приложении напряжения. По аналогии с резисторами и индуктивностями, закон Ома можно применить и к конденсаторам. Однако в данном случае, напряжение на конденсаторе обратно пропорционально току, протекающему через него, и пропорционально его емкости. Таким образом, сила тока в цепи с конденсатором определяется сопротивлением и напряжением на элементе.

Расчет пассивных элементов электрической цепи

Первым шагом в расчете пассивных элементов является определение необходимых значений и параметров элементов. Для резисторов это может быть сопротивление, для конденсаторов — емкость, а для индуктивностей — индуктивность. Имея эти значения, мы можем приступить к расчету и определению влияния этих элементов на поведение цепи.

Для резисторов основной параметр, который следует учесть, это сопротивление, которое измеряется в омах. При расчете резисторов необходимо учитывать их влияние на поток тока и напряжение в цепи. Конденсаторы, с другой стороны, характеризуются емкостью, измеряемой в фарадах. Они обладают способностью накапливать электрический заряд и влиять на изменение напряжения в цепи. И наконец, индуктивности имеют индуктивность, измеряемую в генри, и они влияют на ток в цепи, за счет создания электромагнитного поля.

Резисторы

Сопротивление
Влияние на ток и напряжение в цепи

Конденсаторы

Емкость
Влияние на изменение напряжения в цепи

Индуктивности

Индуктивность
Влияние на ток в цепи

При расчете пассивных элементов цепи необходимо учитывать их сочетание и взаимодействие с другими элементами. Это может включать расчет импеданса цепи, временные константы для зарядки и разрядки конденсаторов, а также взаимное индуктивное влияние между различными индуктивными элементами.

Вычисление сопротивления резистора с помощью закона Ома

Вычисление сопротивления резистора осуществляется на основе закона Ома, который утверждает, что сила тока, протекающего через резистор, пропорциональна напряжению на его клеммах. С помощью формулы, основанной на законе Ома, можно вычислить сопротивление резистора, зная значения напряжения и силы тока.

Сопротивление резистора измеряется в омах (Ω) и может быть определено с помощью формулы R = U/I, где R обозначает сопротивление, U — напряжение на клеммах резистора, а I — сила тока, протекающая через него. Данная формула позволяет определить сопротивление резистора без необходимости его разборки или специальных измерительных инструментов.

Вычисление сопротивления резистора является важным этапом при проектировании и расчете электрических цепей. Знание сопротивления резисторов позволяет определить электрические параметры цепи, такие как мощность, ток и напряжение. Это необходимо при выборе подходящих резисторов для конкретной электрической схемы, а также при оценке их потенциального влияния на работу цепи в целом.

Расчет величин индуктивности и емкости в цепи с учетом основного электротехнического принципа

Индуктивность – это способность цепи сопротивляться изменению электрического тока. Она может быть образована различными устройствами, например, катушками индуктивности. Расчет индуктивности в цепи основывается на принципе, что изменение тока через индуктивную нагрузку создает электромагнитное поле, которое в свою очередь создает электродвижущую силу, противодействующую этому изменению. Таким образом, чем больше индуктивность, тем больше будет электродвижущая сила против изменения тока.

Емкость, с другой стороны, представляет собой способность цепи принимать и хранить электрический заряд. Расчет емкости в цепи основывается на принципе, что заряды, накопленные на конденсаторе, создают электродвижущую силу, вызывающую противодействие любому изменению тока. Чем больше емкость, тем больше будет электродвижущая сила против изменения тока.

Параметр	Определение	Расчет
Индуктивность	Способность цепи сопротивляться изменению тока	Определение через физические характеристики и расчет с использованием величины сопротивления в цепи
Емкость	Способность цепи принимать и хранить электрический заряд	Определение через физические характеристики и расчет с использованием величины сопротивления в цепи

Расчет величин индуктивности и емкости в цепи с учетом основного электротехнического принципа, связанного с законом Ома, имеет существенное значение при проектировании и анализе различных электрических систем. Понимание взаимосвязи этих параметров и сопротивления в цепи позволяет оптимизировать эффективность работы системы и добиться требуемых результатов.

Примечания и ограничения при использовании закона Ома для пассивных элементов

При применении закона Ома для пассивных элементов, таких как резисторы, индуктивности и емкости, существуют ряд важных примечаний и ограничений. Понимание и учет этих факторов играют ключевую роль в достижении точности и надежности измерений в электрических цепях.

Температурные изменения:
Важно учитывать, что сопротивление, индуктивность и емкость пассивных элементов могут изменяться в зависимости от температуры окружающей среды. Поэтому, при анализе электрической цепи, необходимо учесть потенциальное влияние температурных изменений на точность измерений.
Частотные ограничения:
Для некоторых пассивных элементов, закон Ома может оказаться не совсем точным при работе с сигналами высокой частоты или переменного тока. Например, в случае индуктивности и емкости, сопротивление и реактивное сопротивление могут изменяться в зависимости от частоты. Поэтому, при проектировании и анализе цепей, необходимо учитывать частотные ограничения для достижения точных результатов.
Точность элементов:
Пассивные элементы, как и все компоненты электрических цепей, имеют производственные отклонения и некоторую погрешность. При применении закона Ома, важно учитывать точность этих элементов для получения достоверных результатов и предотвращения некорректных измерений.
Влияние внешних факторов:
В работе пассивных элементов может быть замечено влияние окружающей среды, магнитных полей, электромагнитных помех и других внешних факторов. Это может приводить к искажению измерений и несоответствию с предсказуемым поведением электрической цепи. Поэтому, для детального анализа и минимизации влияния внешних факторов, требуется провести специальные эксперименты и использовать соответствующие экранирования и устранения помех.

В целом, при использовании закона Ома для анализа пассивных элементов необходимо учитывать возможные изменения сопротивления, индуктивности и емкости в зависимости от температуры и частоты, точность элементов и влияние внешних факторов. Это поможет достичь более точных и надежных результатов в измерениях и анализе электрических цепей.