Закон Ома для резисторов — понятное объяснение основного электрического закона без использования точек и двоеточий

Устройства, анализ и эксплуатация электрических цепей являются одной из основ инженерной науки. Системы сопротивлений, невидимые на первый взгляд, словно играют важнейшую игру в организации потока электрической энергии. И в этой игре ведущую роль играют резисторы, элементы цепи, которые обладают особыми свойствами и подчиняются Закону столь же точно, как стрелка указательных весов подчиняется гравитации.

В основе понимания закона, облегчающего рассмотрение и расчет электрических цепей, лежат простые и универсальные принципы. Однако, когда мы проводим общий анализ составляющих резисторов, кажется, что их суть гораздо сложнее, содержит таинственность. Но не стоит поддаваться этим иллюзиям и забывать о реальности: резисторы — верные и предсказуемые «солдаты» электрического тока, венцом их работы становится закон, впервые сформулированный в 1827 году немецким физиком Георгом Симоном Омом.

Объяснять закон Ома – значит раскрывать перед нами универсальные числовые закономерности, связывающие ток, напряжение и сопротивление. Они, как чередующиеся ноты в гармонии, становятся ключом к пониманию и регулированию электрических систем. И также, как землетрясения могут потрясти стабильность нашего мира, изменения электрического тока и сопротивления в электрической цепи изменяют динамику и функционирование систем, которые мы ежедневно используем в нашей жизни.

Основные принципы и формулы Закона Ома: путь электрического тока в резисторах

Суть закона Ома заключается в следующем: при константном сопротивлении в цепи, сила тока, протекающего через нее, прямо пропорциональна напряжению, которое создается в этой цепи. Иными словами, сопротивление резистора представляет собой меру его способности сопротивляться току, и это сопротивление определяет величину тока, протекающего через резистор при заданном напряжении.

Если обозначить сопротивление резистора как R, напряжение на нем как U, а ток, протекающий через резистор, как I, Закон Ома представляется в виде следующей формулы: U = I * R.

Формула Закона Ома позволяет рассчитать одну из величин – ток, если известны другие две – напряжение и сопротивление. Также, зная две известные величины, можно рассчитать недостающую третью. Для этого достаточно переставить формулу и выразить нужную величину в зависимости от других двух.

Резисторы: принцип работы и влияние на электрическую цепь

В этом разделе мы поговорим о компонентах электрической цепи, которые вносят определенное сопротивление и оказывают существенное влияние на прохождение электрического тока. Речь пойдет о резисторах, которые нередко встречаются в наших повседневных устройствах, их функции и особенности работы.

Резисторы, также известные как сопротивления, представляют собой электронные компоненты, обладающие способностью ограничивать или регулировать поток электрического тока в цепи. Они могут быть различных форм, размеров и материалов, их основное назначение – создание определенного уровня сопротивления электрическому току.

Когда электрический ток проходит через резистор, он сталкивается с внутренним сопротивлением, которое препятствует свободному движению зарядов. Это «тернистый путь» зарядов через резистор усиливает влияние резистора на цепь, внося в нее эффекты, такие как изменение напряжения и температуры. Некоторые резисторы также обладают свойством изменять свое сопротивление при различных условиях, и могут быть использованы для контроля и регулировки электрической силы тока.

Важно понимать, что резисторы не только выполняют функцию управления потоком электричества, но и могут служить вспомогательными элементами для защиты других компонентов цепи. Например, они могут использоваться для предотвращения перепада электрического напряжения, слишком большого тока или перегрузки цепи в целом.

Таким образом, резисторы являются неотъемлемой частью электрической цепи, и их принцип работы и влияние на цепь играют важную роль в обеспечении стабильности и контроля потока электронов. Понимание этих основных принципов поможет углубить знания в области электроники и научиться эффективно работать с резисторами в различных устройствах и системах.

Значение резистора в электрической цепи

Резистор, как яркий представитель этой категории компонентов, обладает высокой электрической сопротивляемостью – своего рода силой, препятствующей протеканию тока. При этом резистор обеспечивает стабильность напряжения и тока в цепи, предотвращая перегрузку и перегрев других элементов. Благодаря своим характеристикам, резистор выполняет важную функцию в электрической цепи, обеспечивая баланс и безопасность работы всей системы.

Основные характеристики резисторов: сопротивление и мощность

Мощность резистора — это количество энергии, которую он может поглотить или выделять. Мощность резистора зависит от сопротивления и напряжения, подаваемого на него. Высокая мощность означает, что резистор может справляться с большим количеством энергии без перегрева. Мощность резистора важна при выборе резистора для конкретных электрических цепей, чтобы избежать его перегрузки и повреждения.

Таким образом, сопротивление и мощность являются основными характеристиками резисторов. Зная эти параметры, можно определить, как резистор влияет на ток и энергию в электрической цепи, а также выбрать подходящий резистор для конкретных задач и условий эксплуатации.

Равенство сопротивления и тока: применение Омовского закона

Равенство сопротивления и тока обозначает простую и важную идею: чем больше сопротивление в данной цепи, тем меньше ток будет протекать через нее.

Правило Ома гласит, что сила тока (I), протекающая через резистор, пропорциональна напряжению (U) на нем, и обратно пропорциональна его сопротивлению (R). Это можно выразить математически с помощью формулы I = U/R. Данное соотношение позволяет нам расчетно определить величину тока, напряжения или сопротивления в заданной ситуации.

При использовании Омовского закона необходимо учитывать, что сопротивление может варьироваться в зависимости от материала, формы и длины проводников. Также следует помнить о температурных изменениях, которые могут влиять на сопротивление резистора.

Чрезвычайно важно понимать и применять Омовский закон при проектировании и обслуживании электрических систем. Знание этого закона позволяет эффективно рассчитывать параметры цепей, контролировать и стабилизировать ток, а также предотвращать непредвиденные ситуации, связанные с перегрузкой или неправильным функционированием резисторов.

Принцип работы и формула, описывающая взаимодействие элемента сопротивления с электрическим током

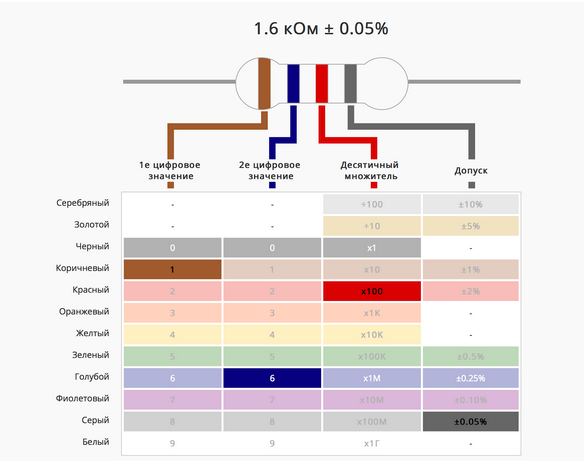
Омовский закон формулирует зависимость между напряжением, протекающим через элемент сопротивления, и силой тока, протекающей через него. Этот закон был открыт и впервые сформулирован немецким физиком Георгом Омом в 1827 году, и он является одним из основных принципов в электрических цепях.

Основная формула закона Ома связывает силу тока, напряжение на элементе сопротивления и его сопротивление. Формула выглядит следующим образом:

Формула	Описание
U = I * R	Напряжение на элементе сопротивления (U) равно произведению силы тока (I) на сопротивление (R)

Следуя Омовскому закону, сила тока, протекающего через элемент сопротивления, прямо пропорциональна напряжению на нем и обратно пропорциональна его сопротивлению. Именно этот феномен позволяет управлять электрическими цепями, регулируя силу тока при изменении напряжения или меняя сопротивление элементов.

Примеры расчетов с использованием принципа Ома

В данном разделе представлены практические примеры расчетов с использованием основного принципа электрической цепи, который был сформулирован Георгом Симоном Омом. Омовский закон позволяет определить линейную зависимость между электрическим током, напряжением и сопротивлением в резисторе.

Рассмотрим первый пример: у нас имеется резистор с известным сопротивлением, и нам необходимо определить значение электрического тока, протекающего через этот резистор при заданном напряжении. Для этого мы можем использовать формулу, основанную на Омовском законе:

• Известно сопротивление резистора: R = 100 Ом.
• Задано напряжение: U = 12 В.
• Используя формулу I = U / R, получаем значение тока: I = 12 В / 100 Ом = 0.12 А.

Второй пример связан с определением сопротивления резистора на основе известных значений напряжения и тока. Для расчета используем формулу R = U / I:

• Известно напряжение: U = 24 В.
• Известно значение тока: I = 0.5 А.
• Подставляя значения в формулу, получаем: R = 24 В / 0.5 А = 48 Ом.

Третий пример демонстрирует расчет напряжения на резисторе при заданном значении сопротивления и токе с использованием формулы U = R * I:

• Известно сопротивление: R = 150 Ом.
• Известно значение тока: I = 0.3 А.
• Подставляя значения в формулу, получаем: U = 150 Ом * 0.3 А = 45 В.

Приведенные примеры позволяют наглядно продемонстрировать применение Омовского закона в практических расчетах. Помимо указанных, существуют и другие формулы, основанные на этом законе, которые позволяют определить различные величины электрической цепи для резисторов и других устройств.

Видео:

КАК ПОНЯТЬ ЗАКОН ОМА | ОБЪЯСНЯЮ НА ПАЛЬЦАХ

Конструктор Знаток. Основные понятия о сопротивлениях.