Закон Ома — объяснение и применение в замкнутых участках цепи для расчета электрических сил и сопротивлений

В нашем стремительно развивающемся мире использование электричества становится все более неотъемлемой частью нашей повседневной жизни. При погружении в эту захватывающую область, важно понимать основы электрической теории и применять законы, описывающие поведение электрических систем.

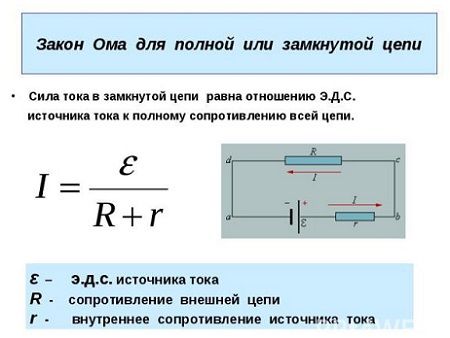
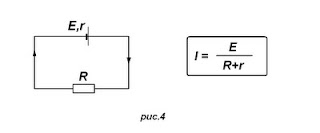
Одна из важнейших концепций в этой области — закон ома для замкнутого участка электрической цепи. Этот закон, открытый ученым еще в 1827 году, описывает взаимосвязь между током, напряжением и сопротивлением в электрической цепи. С его помощью можно расчетно оценить, как изменяется ток в цепи при изменении напряжения или сопротивления.

Идея закона Ома заключается в том, что ток, протекающий по замкнутому участку цепи, пропорционален напряжению, приложенному к этому участку, и обратно пропорционален сопротивлению цепи. Другими словами, если увеличить напряжение в цепи, то ток будет расти, при условии, что сопротивление цепи остается постоянным.

Таким образом, закон ома позволяет установить линейную связь между током, напряжением и сопротивлением. Это позволяет электронным инженерам и электрикам предсказывать и контролировать токи в электрических системах, зная значение напряжения и сопротивления цепи.

Изучение закона ома для замкнутого участка цепи является базовым шагом в понимании электрических систем. Это помогает строить эффективные и безопасные системы электропитания, а также создавать новые устройства и технологии, которые преображают нашу жизнь ежедневно.

Применение закона Ома в электрических цепях: основные принципы и практические примеры

Ключевой идеей закона Ома является установление связи между электрическим током, силой тока и сопротивлением в проводнике. В соответствии с этим законом, сила тока, протекающего через замкнутый контур, прямо пропорциональна напряжению и обратно пропорциональна сопротивлению проводника.

Применение закона Ома в электрических цепях позволяет рассчитывать и оптимизировать параметры цепи с целью достижения желаемого электрического эффекта. Например, основываясь на законе Ома, можно определить максимально возможную силу тока в цепи при заданном напряжении и сопротивлении. Также он используется для расчета энергопотребления в различных устройствах и системах, а также для оптимизации электропроводности и эффективности электрических устройств.

Понимание и применение закона Ома позволяет инженерам и электрикам эффективно работать с электрическими цепями, обеспечивая их безопасность и надежную работу.

Основные понятия — Ток, сопротивление и напряжение

В данном разделе рассмотрим основные понятия, которые играют важную роль в контексте закона Ома для замкнутого участка электрической цепи.

Ток – это основной параметр электрической цепи, который описывает движение заряда через проводники. Величина тока показывает, сколько зарядов проходит через секцию цепи за единицу времени. Ток измеряется в амперах (А).

Сопротивление – это мера сопротивления проводников движению заряда. Сопротивление зависит от материала проводника, его физических характеристик и геометрии. Чем выше сопротивление, тем сложнее для зарядов преодолеть это препятствие. Сопротивление измеряется в омах (Ω).

Напряжение – это разность потенциалов между двумя точками электрической цепи. Оно является причиной движения заряда и создает электрическое поле, по которому заряды перемещаются. Напряжение можно представить как силу, способствующую движению заряда. Напряжение измеряется в вольтах (В).

Из понятий тока, сопротивления и напряжения составляется закон Ома, который описывает взаимосвязь между этими величинами на замкнутом участке цепи. Важно понимать эти основные понятия для более глубокого изучения работы электрических цепей и применения закона Ома в решении задач электротехники.

Математическая формулировка — Связь тока, сопротивления и напряжения

Изучение взаимосвязи тока, сопротивления и напряжения позволяет понять, как электрическая энергия передается через проводники и элементы цепи, а также как она воздействует на электрические устройства. Например, когда ток проходит через электрическую лампу, сопротивление внутри лампы преобразует электрическую энергию в световую и тепловую. Знание математической формулировки позволяет рассчитать, сколько тока протекает через цепь при заданном напряжении и сопротивлении, а также предсказать изменения величин при изменении параметров цепи.

Идея математического описания взаимосвязи тока, сопротивления и напряжения выражается в формуле, где сила тока (I) пропорциональна напряжению (U) и обратно пропорциональна сопротивлению (R). Такая зависимость может быть выражена следующим образом: I = U/R. Эта формула позволяет вычислить силу тока, напряжение или сопротивление, если известны две другие величины. Она является основным инструментом для анализа и расчета электрических цепей и позволяет предсказывать изменения величин при изменении параметров цепи.

Закономерности электрического тока на замкнутых участках схемы

Независимо от конкретных элементов и соединений, электрическая цепь может быть разделена на замкнутые участки, где осуществляется передача электрического тока. В этих участках действуют определенные закономерности, которые позволяют понять и описать происходящие процессы.

• Сила тока на замкнутом участке. Величина, характеризующая интенсивность электрического тока, может быть разной на разных участках цепи. Она зависит от сопротивления участка и напряжения, поданного на цепь. Более сопротивляемые участки будут иметь меньшую силу тока, а величина силы тока на замкнутом участке будет обратно пропорциональна его сопротивлению.
• Напряжение на замкнутом участке. Оно представляет собой разницу потенциалов между двумя точками участка и обозначает энергетическую силу тока. Напряжение может быть как постоянным, так и переменным в случае применения переменного тока. Оно определяет, какая часть энергии будет потрачена на преодоление сопротивления участка и какая часть будет использована для выполнения работы в цепи.
• Закон Кирхгофа. На каждом участке цепи сумма электрических токов, втекающих и исходящих, равна нулю. Это означает, что электрический ток, протекающий через каждый участок цепи, одинаковый в разных точках участка.
• Распределение тока в разветвленных цепях. При наличии разветвлений электрический ток делится между параллельными участками цепи. Здесь важна сопротивляемость каждого участка: чем больше сопротивление, тем меньше ток протекает через данный участок.

Изучение этих закономерностей позволяет более глубоко понять свойства и поведение электрического тока на замкнутых участках цепи и применять их для решения различных электротехнических задач.

Определение сопротивления отрезка проводника

В данном разделе рассмотрим методы определения сопротивления участка электрической цепи без прямого ссылания на Закон Ома для замкнутого участка. Здесь представлены способы измерения и вычисления сопротивления, которые позволяют определить электрическое сопротивление проводника часто используемыми и доступными инструментами.

Методы измерения сопротивления

Первый метод основан на использовании амперметра и вольтметра. Для этого измеряется сила тока, протекающего через участок цепи, и напряжение на этом участке. Затем сопротивление вычисляется по формуле, устанавливающей связь между током и напряжением. Второй метод основан на применении мостовых схем, таких как мост Витстона. Этот метод позволяет получить более точное измерение сопротивления путем сравнения с известным сопротивлением.

Вычисление сопротивления по характеристикам материала

Известно, что сопротивление проводника зависит от его материала. Этот факт позволяет определить сопротивление на основе характеристик материала проводника, таких как удельное сопротивление и геометрические параметры. Для этого используются формулы и таблицы, которые позволяют вычислить сопротивление в зависимости от этих параметров.

Практические примеры

В этом разделе представлены примеры практического определения сопротивления участка цепи с помощью различных методов и подходов. Примеры включают расчеты с использованием известных формул и проведение экспериментов с применением современных инструментов и приборов. Это позволяет получить более наглядное представление о процессе определения сопротивления и его значении в электрических цепях.

Расчет электрического тока и напряжения на участке: принципы и методы

В данном разделе рассмотрим методы и принципы расчета электрического тока и напряжения на заданном участке электрической цепи. Проанализируем взаимосвязь между этими физическими величинами и опишем основные законы, которые позволяют проводить точные расчеты.

Для начала изучим основные понятия, которые необходимо усвоить перед проведением расчетов. Определим сопротивление, электрический ток и напряжение, а также установим их взаимосвязь. Далее, с посредством простых примеров и теоретических формул, описанных в таблице, будем научены считать значения электрического тока и напряжения на участке цепи. В результате, будем способны определить электрический ток для заданного значения напряжения, а также рассчитывать напряжение для данной силы тока.

Видео:

Условия существования постоянного тока. Закон Ома для участка цепи. 10 класс.

КАК ПОНЯТЬ ЗАКОН ОМА | ОБЪЯСНЯЮ НА ПАЛЬЦАХ

Рекомендуем:

Закон Ампера: простыми словами – определение, формула, применение Как правильно подключить плавный пуск на электропилу: пошаговая инструкция 2 закон ома формула — что это такое, как ее применять и почему она важна для понимания электрических цепей Экспертные советы — как точно определить исправность конденсатора без использования сложного оборудования Символика и значения цветов — Желтый, черный, синий и зеленый Основные факторы и методы расчета затирки для мозаичных покрытий – секрет успеха в создании стильных и долговечных интерьеров Закладная в гипсокартоне — как правильно установить и использовать Как выбрать правильное сечение кабеля для электроплиты и обеспечить безопасность и эффективность работы Идеальное решение для участка с деревянным домом — как выбрать и установить унитаз, подходящий по стилю и функциональности к вашему уютному жилищу Как выбрать автомат для подключения электрооборудования мощностью 5 кВт и трёхфазным напряжением?